Bitcoin est un réseau P2P sur internet qui permet aux participants de partager une base de données de transactions. Un bitcoin (ou une fraction de bitcoin) passe d'une adresse à une autre grâce à un message de transaction signé par le propriétaire de l'adresse bitcoin d'origine. Une transaction est vérifiée et pourra être inscrite dans la base de données commune si une chaîne de signatures authentiques permet de remonter toutes les transactions précédentes jusqu'à la création de chacun des bitcoins qui composent le montant de la transaction. Rappelons que les bitcoins sont créés par une transaction spéciale appelée "coinbase transaction" dans chaque nouveau bloc ajouté à la base de données.

Le mécanisme de signature des transactions et leur vérification est l'algorithme ECDSA ("Elliptic Curve Digital Signature Algorithm") qui joue donc un rôle crucial dans la technologie bitcoin. ECDSA assure aussi la génération des paires de clés (clé privée et clé publique) nécessaire aux signatures: toute adresse bitcoin est dérivée d'une clé publique ECDSA.

L’algorithme ECDSA a été démontré comme sûr cryptographiquement en 2001 et a été publié comme norme internationale dans le document ANSI X9.62.

La sécurité de RSA dépend de la difficulté de factoriser un grand nombre entier.
Celle de ECDSA repose sur la difficulté de calculer le «logarithme» discret d’un grand nombre entier, c’est à dire connaissant a = bⁿ comment retrouver n, le logarithme de a en base b.
ECDSA utilisé avec des clés de 256 bits dans bitcoin offre une sécurité comparable à RSA sur 3072 bits.

Voici comment fonctionne l’algorithme ECDSA pour la génération d’une paire de clés, la fabrication d’une signature avec la clé privée et la vérification de cette signature avec la clé publique.

ECDSA utilise un ensemble fini de points (x,y) où x et y sont entiers et vérifient une équation du type:
y² = (x³ + ax + b) [mod n]
ECDSA utilise par ailleurs une loi de groupe qu’on pourrait appeler l’«addition» de deux points P et Q sur la courbe, ainsi définie: P+Q = R quand on trace une droite entre P et Q qui coupe la courbe au point S et quand R est le symétrique de S sur la courbe, par rapport à l’axe des x.


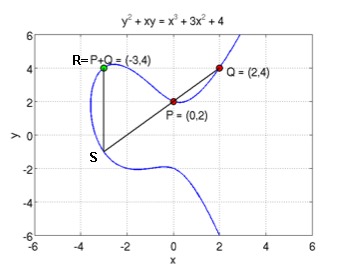
La construction de R se traduit algébriquement par les équations:
x_R = L² - x_P - x_Q and,
y_R = L(x_P - x_R) - y_P and,
L = (y_Q - y_P)/(x_Q - x_P)

Quand P et Q se rapprochent, la droite PQ tend vers la tangente à la courbe, donc on peut additionner un point avec lui-même en prenant cette tangente au point P pour construire les points S et R. On a alors R = 2P, 3P= R + P et ainsi de suite de sorte qu’on peut calculer un point kxP où k est un entier quelconque, tant que R ne se trouve pas à l’infini.



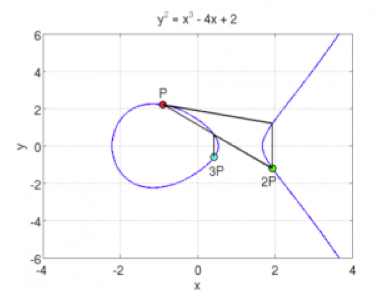
Noter que la courbe définie par y² = (x³ + ax + b) n’est pas une ellipse: les fameuses courbes elliptiques doivent en fait leur nom aux intégrales elliptiques.

L’empreinte M du message à signer est calculée avec la fonction SHA1 qui produit un condensé de 20 octets (160 bits).
En pratique, pour vérifier une signature ECDSA, connaissant le point C = MxG (la signature) et le point de base G, il s’agit de retrouver l’entier M (le condensé du message).
MxG signifie que le point G est «additionné» avec lui-même M fois, l’addition de deux points définissant une loi de groupe sur l’ensemble des points d’un champ fini. Le champ fini comporte un grand nombre de points et, si le point de base G est bien choisi, l’attaque «brute force» consistant à calculer tous les points kxG pour toutes les valeurs possible de k (entier) et à vérifier que l’un de ces points coïncide avec C est impraticable: c’est là que réside la sécurité de ECDSA et donc de bitcoin.

Les paramètres de la courbe doivent être choisis avec soin pour éviter d’utiliser une courbe faible. Par exemple une courbe elliptique «singulière», c’est à dire avec un point singulier comme un point d’intersection de la courbe avec elle-même est considérée comme faible et non utilisable pour une application cryptographique.
Le document FIPS http://csrc.nist. gov/publications/fips/fips186-3/fips_186-3.pdf précise des paramètres sûrs pour des courbes ECDSA robustes et bitcoin utilise une de ces courbes. La courbe utilisée par bitcoin est une courbe dite de Koblitz du nom du cryptographe, Neal Koblitz, qui, en 1985, a démontré l’utilité des courbes elliptiques en cryptographie.
Z_p: champ fini premier où p est un grand nombre premier (p = caractéristique du champ, champ étant un cas particulier d’un anneau)
On considère les points (x,y) où x et y sont dans Z_p et vérifient
y² = (x³ + ax + b) [mod n]
Le nombre de ces points constitue ce qu’on appelle l’ordre de la courbe.
n: ordre du point G, plus petit entier tel que n x G = O (O : élément «identité» du groupe fini). G doit être choisi de sorte que n est un grand nombre entier.
h: cofacteur, l’ordre de la courbe elliptique divisé par n.

k: à chaque signature, le signataire va choisir au hasard un entier k, très grand mais strictement inférieur à n, pour fabriquer sa signature. Noter que cet entier k ne sera pas nécessaire pour vérifier la signature et que k devra être changé à chaque signature. Ne pas changer k à chaque signature est une grosse faille de sécurité car cela peut permettre à une pirate de calculer la clé privée. Cette faille a été exploitée en 2010 contre Sony pour déchiffrer la clé privée qui permet de faire tourner n’importe quel logiciel sur la console PS3.

Génération des clés ECDSA
La première étape de la fabrication d’une signature ECDSA consiste donc à choisir un entier X, strictement plus petit que n, comme clé privée puis à calculer la «clé publique» Y telle que Y = X x G
La clé publique Y est donc en fait un point sur la courbe. Y ainsi que les paramètres p, n, a , b et G doivent être publiés.

Calcul et vérification d’une signature ECDSA

Après avoir calculé le condensé M du message avec la fonction à sens unique SHA1, la signature va se composer de deux parties sig₁ et sig₂. On calcule d’abord sig₁ en calculant le point kxG et ne retenant que sa coordonnée x (modulo n):
sig₁ = (k×G)_x [mod n]
Si le calcul du modulo donne zéro, il faut recommencer avec une autre valeur de k.
On calcule ensuite sig₂ = k⁻¹·(M+X·sig₁) [mod n] où k⁻¹ est l’inverse de k modulo n.

Le destinataire qui reçoit le message et la signature (sig₁, sig₂) peut vérifier l’authenticité du message en calculant d’abord son condensé M via SHA1 puis les nombres
w = sig₂^-1 [mod n]
u₁ = M·w [mod n]
u₂ = sig₁·w [mod n]

enfin en calculant le point
(x,y) = u₁ × G + u₂ ×Y

La signature est vérifiée si sig₁ ≡ x [mod n]

Pour terminer, notons qu’un grand nombre de cerveaux se sont penchés sur la possibilité de concevoir un ordinateur quantique pour attaquer la sécurité des algorithmes comme RSA ou ECDSA. Dans le cas de ECDSA sur 256 bits cependant, il semble que les lois de la thermodynamique ne permettent pas, en l’état actuel des connaissances, de réaliser un tel calcul avant l’extinction du soleil, quelle que soit la machine qui l’exécute: à suivre donc..

Remerciements à Avinash Kak de Purdue University pour les images des courbes provenant de son cours sur les courbes elliptiques.